LovesTheTeam.com

Jums būs nepieciešams

• lineāls, zīmulis.

Instrukcijas

1

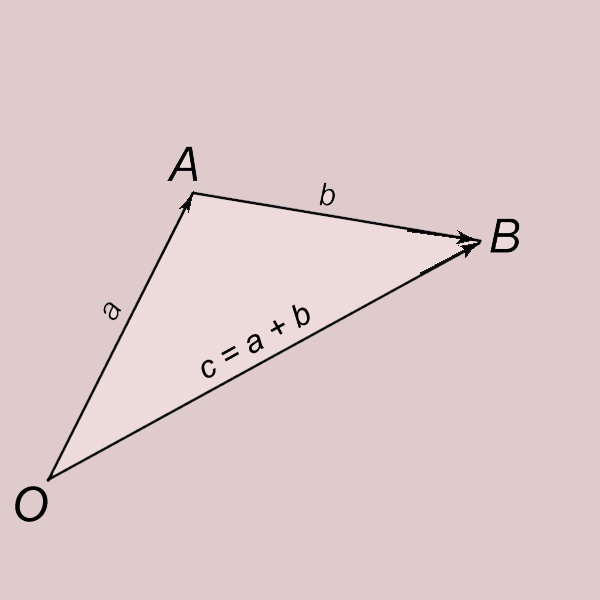
Vektoru pievienošana ar trijstūra noteikumu. Ļaut, ka a un b ir divi no nulles vektori. Mēs atliekam vektoru a no punkta 0 un apzīmē tā beigas ar burtu A. OA = a. Mēs atlikt vektoru b no punkta A un apzīmē tā beigas ar burtu B. AB = b. Vektors ar izcelsmi punktā O un beidzot pie punkta B (OB = c) sauc summu a un b un rakstīt c = a + b. Tiek uzskatīts, ka vektors c ir iegūts, pievienojot vektorus a un b.

2

Summa no diviem noncollinear vektori a un b, var būtLai izveidotu ar noteikumu, ko sauc par paralelogrammu noteikums. Mēs atliekam no punkta A, pārnēsātājus AB = b un AD = a. Vektora beigās izdariet līniju, kas ir paralēla vektoram b, un caur vektora beigām b ir taisna līnija, kas ir paralēla vektoram a. Ļaujiet C punkts konstruētu līniju krustošanās punkts. Vektors AC = c ir vektoru a un b summa. c = a + b.

3

Tiek saukts vektors pretējs vektoram avektors, apzīmē - un tādā veidā, ka vektoru a un vektora s summa ir vienāda ar nulli vektors A + (-a) = 0Vektor pretī vektoru AV, ko dēvē arī BA: BA + AB = AA = 0Nenulevye opposite vektori ir vienāda garuma ( | a | = | -a |) un pretējos virzienos.

4

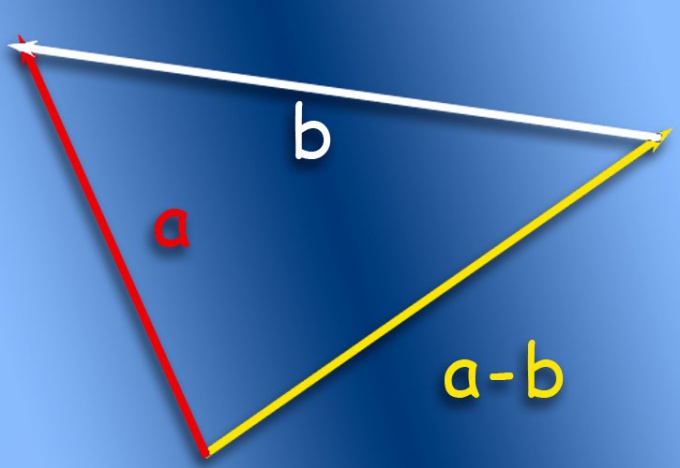
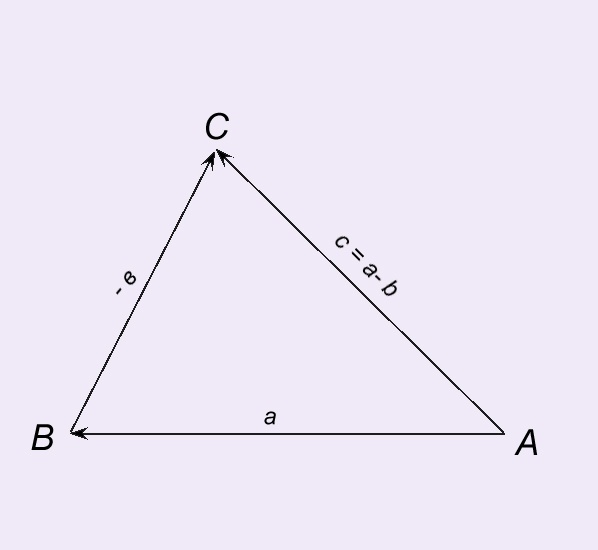
Vektora a summa un vektors pretējsvektors b ir starpība starp diviem vektoriem a-b, ti, vektoru a + (-b). No diviem vektoriem a atšķirība un b apzīmē - b.Raznost diviem vektoriem a un b var iegūt, izmantojot trīsstūra kārtulu. Mēs atlikt vektoru a no punkta A. AB = a. No beigām vektora AB atlikt vektoru BC = -B, vektoru AC = C - atšķirība vektorus un b.s = a - b.

5

Šīs darbības īpašības, pievienojot vektoru: 1) nulles vektors iestādē: a + 0 = a2) associativity par Turklāt: (a + b) + c = a + (b + c); 3) commutativity: a + b = b + a;

Padoms 2: Kā atrast koordinātu summu

Katrs materiāls objekts ieņem vietu kosmosā. Fiziskā ķermeņa koordinātas ir tā izvietojuma skaitliskās īpašības, kas nosaka objektu savstarpējo stāvokli.

Instrukcijas

1

Norādiet objektu koordinātu daudzumunepieciešams atrast koordinātu skaitu. Objekts var būt punkts, kas pārvietojas pa vienu koordinātu asi. Var būt nepieciešams apkopot punktu koordinātas uz plaknes vai telpā.

2

Ja punkti pārvietojas tikai pa taisnu līniju, tad šādiem punktiem ir tikai viena koordinātas. Novietojiet ciparu asi ar līniju, uz kuras tiek pārvietoti izskatāmie objekti.

3

Tagad problēma ir atrast divu vai divu koordinātu summuvairāki punkti tiek samazināti līdz pozitīvo un negatīvo skaitļu pievienošanai. Galvenais punkts ir definīcija atsauci nulles un norāde, kura virzienā no nulles, ir pozitīva, un ko - nē.

4

Plaknes punktu norāda ar diviem parametriem. Lai atrastu punktu koordinātu summu lidmašīnā, pievienojiet divus skaitļus - punkta koordinātas gar OX asi un pa OY asi.

5

Nosakot vektora koordinātu summu uzXOY plakne, vispirms atrast koordinātes sākumā un beigās vektors. No beigām vektoru vērtībām X atņemt X sākums vērtību vektoru. Iegūtais skaitlis ir vektora abscissa. Starpība starp vērtību Y un sākas beigās vektors - koordinātu vektors. Reizes abscisa un saskaņot par vektoru summas vektoru un saņemt koordinātas.

6

Atrast krustpunkta koordinātu summudivas taisnas līnijas vai līknes, vispirms jāatrod šie punkti. Problēma ir atrisināt vienādojumu sistēmu, kas apraksta krustojošās līnijas (līknes). Vienādojumu kopīgās saknes ir sagaidāmie ierobežojošie punkti.

7

Apsverot punktu kosmosā, koordinātu summu nosaka, pievienojot trīs ciparus - daudzumus OX, OY un OZ.